
Zapisy na kursy z zarządzania danymi tylko do końca kwietnia
Już ponad 3500 uczestników korzysta z dostępnych na platformie Navoica pierwszych w Polsce internetowych kursów z zarządzania danymi badawczymi dla naukowców i data stewardów. Za ich przygotowanie odpowiadali eksperci z Platformy Otwartej Nauki ICM UW. Na kursy można zapisywać się do końca kwietnia.
1000 zbiorów w Repozytorium Otwartych Danych
2 lipca 2015 roku rozpoczęło funkcjonowanie pierwsze polskie repozytorium danych badawczych - RepOD. 31 lipca 2015 roku na platformie opublikowano pierwszy zbiór danych. Dziś w repozytorium dostępnych jest już ponad tysiąc zbiorów danych badawczych.
Muzyczna matematyka – matematyczna muzyka
Zapraszamy na XV edycję Matematyki dla Ciekawych Świata, czyli kursu dla uczniów szkół średnich realizowanego wspólnie z Miastem Stołecznym Warszawa. W tym roku wspierać nas będą także Narodowy Instytut Fryderyka Chopina oraz Magazyn Presto, gdyż tematem tej edycji jest: "Muzyczna matematyka - matematyczna muzyka".
Otwarcie Repozytorium Danych Badawczych UW
Już w najbliższy piątek (12 stycznia 2024) odbędzie się inauguracja otwartego repozytorium “Dane Badawcze UW”. Umożliwia ono długoterminowe przechowywanie i udostępnianie danych badawczych. Ułatwia badaczom realizację nakładanych przez grantodawców obowiązków dotyczących zarządzania danymi badawczymi. Stanowi też doskonałe narzędzie promowania efektów pracy badaczy w środowisku naukowym i poza nim.
ICM UW w międzynarodowym konsorcjum MOSAIC
15 instytucji z 7 krajów – Francji, Polski, Portugalii, Kenii, Brazylii, USA i Kolumbii – będzie realizować od nowego roku projekt MOSAIC, dotyczący otwartych, multimodalnych i replikowalnych ekosystemów informacyjnych wspierających społeczności transgraniczne. MOSAIC to jedocześnie pierwsza w Polsce inicjatywa z programu ramowego „Horyzont Europa”, która odnosi się do środowiskowych aspektów zagrożenia epidemiologicznego.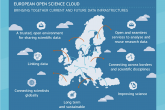
ICM UW wśród zwycięzców przetargu na zamówienie publiczne EOSC w projekcie Horyzont Europa
Komisja Europejska (DG Connect) ogłosiła zwycięzców przetargu na zamówienia publiczne pn. "Usługi zarządzane dla europejskiej platformy chmury otwartej nauki (EOSC)", opublikowanego w ramach Programu Badawczego Infrastruktur Horyzont Europa 2022. ICM UW jest członkiem konsorcjum Open Science Agora, które ma zrealizować pierwszą część zamówienia świadcząc usługi z zarządzania podstawowymi komponentami węzła EOSC UE.
Obliczenia naukowe w ICM
Zdalna stacja robocza, oszczędność czasu, profesjonalne wsparcie techniczne, szkolenia
COVID-19.ICM.EDU.PL
Badania nad zoonozami, Model Epidemiologiczny ICM,
Interaktywna Mapa Pandemii
WOLFRAM, EDELMAN, AFELT, MUTCH, aaronson, …
Zobacz nagrania z Wirtualnych Seminariów ICM z Nauk Obliczeniowych i Informatyki